- 相关推荐
《数学学习的心理基础与过程》读后感
读了《数学学习的心理基础与过程》一书,给我印象最深的是:丹麦数学教育家尼斯认为掌握数学就是拥有数学能力,而数学能力是指能了解、判断、实做、及能在各种不同数学情景与背景下的内外使用数学。他将数学能力结构分为8个方面:数学思维;拟题和解题;数学建模;数学推理;数学表征;符号化与形式化;数学交流;工具的使用。
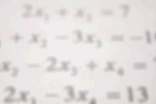
结合这几年的数学教学,我觉得符号化思想在数学课堂教学中需要渗透。数学的思维离不开符号的形式,这样可以大大简化和加速思维的过程。所谓数学符号是指经过数学界约定的规范化的一定形式的数字符号,如定律a·b=b·a。符号化思想方法就是数学信息的载体,也是人们进行定量分析和系统分析的一种载体。在小学数学中常见的数学符号有十多种,常见的有:阿拉伯数字;表示数的字母;表示常数的字母,如π;表示几何形体的;.运算符号;关系符号;结合符号;.约定符号;.性质符号。
数学符号化思想的作用:
1、优化认知结构,如果新知识与原有的数学认知结构中的知识线索相联系,那么通过新旧知识的同化与顺应作用,新知识就被纳入原有的数学认知结构,完成个体对新知识摄入的有意义学习。
2、约简思维过程,比自然语言远为优越的形式化的符号语言,在事实上降低了思维的强度,简化了思维的过程,提高了思维的效率。简单明确的数学符号使数学思维活动能够清晰、准确地进行,容易触发学生的创造性思维。
3、提升建摸能力。在小学数学中渗透符号化思想,将数学符号和数学概念或者数学命题相对应,可以帮助学生着眼于形式,将解决具体问题的思维操作转化为对符号的操作,有利于增强学生建立数学模型的意识,提高解决实际问题的能力。
数学符号化思想数学课堂中的渗透:
1.换元的思想。
这是根据学生的年龄特点和知识水平,采取不同的形式进行渗透,旨在让学生逐步了解换元的思想。例如,解方程组中整体代入,消元,目的是引导学生去思考问题,解决一些有趣的问题,借此,发展学生的思维能力。
2.用字母表示数的思想和列方程解应用题的思想
它的实质是一种抽象化。其目的是为了更深刻地探索、揭示数学规律,达到更准确、更简洁地表达数学规律,在较大范围内肯定数学规律的正确性。比如加法的交换律用a+b=b+a,圆面积用S=πr2表示等。
3、利用数材,重视语义分析。
在实际教学中,充分挖掘教材的教学价值。首先在理解数学概念时既要注意概念与实际对象的联系。又要注意概念与相关符号的联系,搞清每个数学符号的含义与实质;其次要正确领悟教材中出现的一些合成、分解、推出符号,帮助学生理解运算算理及读懂题目的意图。
4、贯穿始终,加大语言互译。
培养学生的符号意识,必须有目的、有意识、有计划、有步骤地渗透于数学教学的始终。在日常教学数学概念、公式、定律和法则时,要加大数学语言的表述与互译,帮助学生多次进行数学符号语言和日常语言的转换,常将日常语言叙述的数量关系或空间形式转化为数学符号语言,并逐步训练学生看懂抽象的符号所反映的数量关系、空间形式和现实含义,用符号语言进行数学交流。
5、把握契机,激发联想活动。
首先,根据数学符号的抽象化、层次化特点。可以由代表数字的字母符号联想到代表抽象元素的字母符号;由几个字母符号联想到多个字母符号;由字母符号的简单组合联想到复杂组合等等。其次,对数学符号进行横向联想,即由眼前的数学对象联想到相关对象。
6.注重引导,构建心智图像。
具有整体识别性、个体差异性的心智图像是形象思维的最高层次,既有具体直观的感性形象成分,又初步具有理性思维的抽象成分,是连接形象思维和抽象思维的纽带,更是问题解决过程中深层次的符号。善于构建正确、清晰的心智图像是具有符号化意识的初步。因此,教师要遵循儿童心理发展规律,有计划、有步骤地正确引导、帮助学生在数学学习中构建心智图像。如,教师有意识引导学生画线段图解决小学数学中的复合应用题;有意识训练学生用自创符号(图形、标号)来表达题意,从而便于解答等等。
【《数学学习的心理基础与过程》读后感】相关文章:
高考数学基础学习技巧及方法10-08
心理学基础知识学习方法10-26
心理学基础10-26
优化复习过程初中数学学习方法10-08
初一数学基础学习方法10-05
基础心理学结构10-26
基础心理学ppt10-26
基础心理学知识11-15
基础数学教学论文10-11
心理学基础入门知识10-26