- 七年级数学有理数的除法的教案 推荐度:
- 相关推荐
七年级数学《有理数的除法》教案(精选10篇)
作为一名优秀的教育工作者,总归要编写教案,编写教案助于积累教学经验,不断提高教学质量。来参考自己需要的教案吧!以下是小编收集整理的七年级数学《有理数的除法》教案,欢迎大家分享。
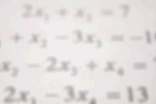
七年级数学《有理数的除法》教案 1
教学目标
1.理解有理数除法的意义,熟练掌握有理数除法法则,会进行运算;
2.了解倒数概念,会求给定有理数的倒数;
3.通过将除法运算转化为乘法运算,培养学生的转化的思想;通过运算,培养学生的运算能力。
教学建议
(一)重点、难点分析
本节教学的重点是熟练进行运算,教学难点 是理解法则。
1.有理数除法有两种法则。法则1:除以一个数等于乘以这个数的倒数。是把除法转化为乘法来解决问题。法则2是把有理数除法纳入有理数运算的统一程序:一确定符号;二计算绝对值。如:按法则1计算:原式;按法则2计算:原式。
2.对于除法的两个法则,在计算时可根据具体的情况选用,一般在不能整除的情况下应用第一法则。如;在有整除的情况下,应用第二个法则比较方便,如;在能整除的`情况下,应用第二个法则比较方便,如,如写成就麻烦了。
(二)知识结构
(三)教法建议
1.学生实际运算时,老师要强调先确定商的符号,然后在根据不同情况采取适当的方法求商的绝对值,求商的绝对值时,可以直接除,也可以乘以除数的倒数。
2.关于0不能做除数的问题,让学生结合小学的知识接受这一认识就可以了,不必具体讲述0为什么不能做除数的理由。
3.理解倒数的概念
(1)根据定义乘积为1的两个数互为倒数,即:,则互为倒数。如:,则2与,-2与互为倒数。
(2)由倒数的定义,我们可以得到求已知数倒数的一种基本方法:即用1除以已知数,所得商就是已知数的倒数。如:求的倒数:计算,-2就是的倒数。一般我们求已知数的倒数很少用这种方法,实际应用时我们常把已知数看作分数形式,然后把分子、分母颠倒位置,所得新数就是原数的倒数。如-2可以看作,分子、分母颠倒位置后为,就是的倒数。
(3)倒数与相反数这两个概念很容易混淆。要注意区分。首先倒数是指乘积为1的两个数,而相反数是指和为0的两个数。如:,2与互为倒数,2与-2互为相反数。其次互为倒数的两个数符号相同,而互为相反数符号相反。如:-2的倒数是,-2的相反数是+2;另外0没有倒数,而0的相反数是0。
4.关于倒数的求法要注意:
(1)求分数的倒数,只要把这个分数的分子、分母颠倒位置即可。
(2)正数的倒数是正数,负数的倒数仍是负数。
(3)负倒数的定义:乘积是-1的两个数互为负倒数。
七年级数学《有理数的除法》教案 2
一、素质教育目标
(一)知识教学点
1.了解有理数除法的定义。
2.理解倒数的意义。
3.掌握有理数除法法则,会进行有理数的除法运算。
(二)能力训练点
1.通过有理数除法法则的导出及运算,让学生体会转化思想。
2.培养学生运用数学思想指导思维活动的能力。
(三)德育渗透点
通过学习有理数除法运算、感知数学知识具有普遍联系性、相互转化性。
(四)美育渗透点
把小学算术里的乘法法则推广到有理数范围内,体现了知识体系的完整美。
二、学法引导
1.教学方法:遵循启发式教学原则,注意创设问题情境,精心构思启发导语并及时点拨,使学生主动发展思维和能力。
2.学生学法:通过练习探索新知→归纳除法法则→巩固练习
三、重点、难点、疑点及解决办法
1.重点:除法法则的灵活运用和倒数的.概念。
2.难点:有理数除法确定商的符号后,怎样根据不同的情况来取适当的方法求商的绝对值。
3.疑点:对零不能作除数与零没有倒数的理解。
四、课时安排
1课时
五、教具学具准备
投影仪、自制胶片、彩粉笔。
六、师生互动活动设计
教师出示探索性练习,学生讨论归纳除法法则,教师出示巩固性练习,学生以多种形式完成。
七、教学步骤
(一)创设情境,复习导入
师:以上我们学习了有理数的乘法,这节我们应该学习有理数的除法,板书课题。
【教法说明】有理数的除法同小学算术中除法一样—除以一个数等于乘以这个数的倒数,所以必须以学好求一个有理数的倒数为基础学习有理数的除法
(二)探索新知,讲授新课
倒数
【教法说明】在有理数乘法的基础上,学生很容易地做出这几个题目,在题目的选择上,注意了数的全面性,即有正数、0、负数,又有整数、分数,在数的变化中,让学生回忆、体会出求各种数的倒数的方法。
师问:两个数乘积是1,这两个数有什么关系?
学生活动:乘积是1的两个数互为倒数(板书)
师问:0有倒数吗?为什么?
学生活动:通过题目0×()=1得出0乘以任何数都不得1,0没有倒数。
师:引入负数后,乘积是1的两个负数也互为倒数,如-4与,与互为倒数,即的倒数是。
提出问题:根据以上题目,怎样求整数、分数、小数的倒数?
【教法说明】 教师注意创设问题情境,让学生参与思考,循序渐进地引出,对于有理数也有倒数是。对于怎样求整数、分数、小数的倒数,学生还很难总结出方法,提出这个问题是让学生带着问题来做下组练习。
【教法说明】例2是检查学生对有理数除法法则的灵活运用能力,并渗透了除法、分数、比可互相转化,并且通过这种转化。
七年级数学《有理数的除法》教案 3
一、知识与技能
掌握有理数除法法则,会进行有理数的除法运算以及分数的化简。
二、过程与方法
通过学习有理数除法法则,体会转化思想,会将乘除混合运算统一为乘法运算。
三、情感态度与价值观
培养学生勇于探索积极思考的良好学习习惯。
四、教学重、难点与关键
1.重点:正确应用法则进行有理数的除法运算。
2.难点:灵活运用有理数除法的两种法则。
3.关键:会将有理数的除法转化为乘法。
五、教学过程,课堂引入
1.小学里,除法的意义是什么?它与乘法有什么关系?
已知两数的积与一个因数,求另一个因数。用除法,乘法与除法互为逆运算除以一个数等于乘以这个数的倒数。
2.求下列各数的`倒数:
(1)-;
(2)-0.125;
(3)-1
六、新授
引入负数后,如何计算有理数的除法呢?
例如8(-4)。
根据除法意义,这就是要求一个数,使它与-4相乘得8
因为 (-2)(-4)=8
所以 8(-4)=-2 ①
另外,我们知道,8(-)=-2 ②
由①、②得 8(-4)=8(-) ③
③式表明,一个数除以-4可以转化为乘以-来进行,即一个数除以-4,等于乘以-4的倒数-
探索:换其他数的除法进行类似讨论,是否仍有除以a(a0)可以转化为乘以呢?[例如(-10)(-4)]
从而得出有理数除法法则:
除以一个不等于0的数,等于乘以这个数的倒数。
这个法则也可以表示成:
七年级数学《有理数的除法》教案 4
设计理念
1.注意突出学生的自主探索,通过一些熟悉的、具体的事物,让学生在观察、思考、探索中体会有理数的意义,探索数量关系,掌握有理数的运算。教学中要注重让学生通过自己的活动来获取、理解和掌握这些知识。
2.本课注意降低了对运算的.要求,尤其是删去了繁难的运算。注重使学生理解运算的意义,掌握必要的基本的运算技能。
教学目标知识与技能:
1.使学生理解有理数倒数的意义。
2.使学生掌握有理数的除法法则,能够熟练地进行除法运算。
过程与方法:
培养学生观察、归纳、概括及运算能力。
情感态度、价值观:
让学生感知数学来源于生活,培养学生学习数学的兴趣。
重点
有理数除法法则。
难点
(1)、商的符号的确定;
(2)、0不能作除数的理解。
教学过程
一、复习引入
1.叙述有理数乘法法则
2.叙述有理数乘法的运算律。
3.计算:
①(―6)
②
③(―3)(+7)―9(―6)
④
二、自主学习计算:
8
尝试
8(- )
1.师生共同研究有理数除法法则:
①问题:
一个数与2的乘积是-6,这个数是几?你能否回答?这个问题写成算式有两种:
2( ?)=-6, (乘法算式)
也就是 (-6)2=( ?) (除法算式)
由2(-3)=-6,
我们有(-6)2=-3。另外,我们还知道: (-6) =-3。
所以,(-6)2=(-6) 。这表明除法可以转化为乘法来进行。
七年级数学《有理数的除法》教案 5
学习目标:
理解有理数除法的意义,掌握有理数除法法则,会进行有理数除法运算。
学习重点:
正确运用有理数除法法则进行有理数除法运算。
学习难点:
寻找有理数除法转化为有理数乘法的方法和条件。
教学方法:
引导、探究、归纳与练习相结合
教学过程
活动一探讨有理数除法法则:
独立完成——合作交流——展示成果
阅读课本P35例5以上的内容,谈谈有理数除法法则是如何得出的?换其他数的除法进行类似讨论,是否任有除
目标导行:
1.理解除法的意义、除法是乘法的逆运算。(重点)
2.理解和掌握有理数除法的两个法则,会正确地进行有理数的除法运算。(重点、难点)
思维诊断:
(打“√”或“×”)
(1)0除以任何一个数,都得0。( )
(2)1除以一个非零数就等于乘这个数的倒数。( )
(3)两数相除,商一定小于被除数。( )
(4)两数相除商为正数,则这两个数均为正数。( )
(5)一个不等于0的.有理数除以它的相反数等于-1。( )
【总结提升】有理数相除的方法
1.0除以任何一个不等于0的数,都得0;但0不能作除数.
2.在进行除法运算时,若能整除,则用“两数相除,同号得正,异号得负,并把绝对值相除”;若不能整除,则用“除以一个不等于0的数,等于乘这个数的倒数”.
3.除法算式中的小数常化成分数,带分数化成假分数,便于转化为乘法时约分.
【总结提升】分数化简的方法
1.把分数转化为除法,利用有理数的除法法则进行化简.
2.利用分数的基本性质,分子和分母都乘以同一个数或都除以同一个不为0的数结果不变进行化简.
6.某自行车厂一周计划每日生产400辆自行车,由于人数和操作原因,每日实际生产量分别为405辆、393辆、397辆、410辆、391辆、385辆、405辆.
(1)用正负数表示每日实际生产量与计划量的增减情况.
(2)该自行车厂本周实际共生产多少辆自行车?平均每日实际生产多少辆自行车?
【归纳整合】符号移动法
化简分数仍遵循“同号得正,异号得负”的符号法则,因此可得符号移动法则:分子、分母、分数前面的符号,三者有一个或三个为负,结果为负,有两个为负,结果为正.
七年级数学《有理数的除法》教案 6
一、教学目标
知识与技能:
①使学生在了解乘法的基础上,掌握有理数乘法法则并初步掌握有理数乘法法则的合理性。
②会进行有理数乘法运算。
③了解有理数的倒数定义,会求一个数的倒数。
过程与方法:
①经历探索有理数乘法法则,发展,观察,归纳,猜想,验证的能力以及培养学生的语言表达能力。
②提高学生的运算能力
情感与态度:通过合作学习调动学生学习的积极性,激发学生学习数学的兴趣,提高学生认识世界的水平。
二、教学重点和难点
重点:依据有理数的乘法法则,熟练进行有理数的乘法运算;
难点:有理数乘法中的符号法则。
三、教学过程
(一)创设问题情景,激发学生的求知欲望,复习旧知,导入新课
前面我们学习了有理数的加减法,接下来就应该学习有理数的乘除法。同学们先看下面的问题:甲水库的水位每天升高3㎝,乙水库的水位每天下降3㎝。4天后,甲、乙水库各自水位的总变化量是多少?
如果用正号表示水位的上升、用负号表示水位的下降。那么,4天后,甲水库水位的总变化量是:3+3+3=3×4=12㎝
乙水库水位的总变化量是:(-3)+(-3)+(-3)+(-3)=(-3)×4=-12㎝引出课题:有理数的乘法
(二)学生探索新知,归纳法则
学生分为四个小组活动,进行乘法法则的探索
设蜗牛现在的位置为点O,若它一直都是沿直线爬行,而且每分钟爬行2cm,问:
(1)向右爬行,3分钟后的位置?
(2)向左爬行,3分钟后的位置?
(3)向右爬行,3分钟前的位置?
(4)向左爬行,3分钟前的位置?
(学生思考后回答)要确定蜗牛的位置需要知道:距离和方向。
为了区分方向:我们规定向右为正,向左为负;为区分时间:我们规定现在的`时间前为负,现在的时间后为正。
(1)情形一:蜗牛在现在位置的右边6㎝处。式子表示为:
(+2)×(+3)=+6
数轴表示如右:
(2)情形二:蜗牛在现在位置的左边6㎝处。式子表示为:(-2)×3=-6
数轴表示如右:
(3)情形三:蜗牛在现在位置的左边6㎝处。式子表示为:(+2)×(-3)=-6
数轴表示如右
(4)情形四:蜗牛在现在位置的右边6㎝处。式子表示为:(-2)×(-3)=+6
数轴表示如右:
仔细观察上面得到的四个式子:
(1)(+2)×(+3)=+6
(2)(-2)×3=-6
(3)(+2)×(-3)=-6
(4)(-2)×(-3)=+6
根据你对乘法的思考,你得到什么规律?
(三)学生归纳法则
a.符号:在上述4个式子中,我们只看符号,有什么规律?
(+)×(+)=()同号得
(-)×(+)=()异号得
(+)×(-)=()异号得
(-)×(-)=()同号得
b.任何数与零相乘,积仍为。
(四)师生共同用文字叙述有理数乘法法则。
归纳:有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数与0相乘,积仍为0。
(五)运用法则计算,巩固法则。
例1计算:(1)(-5)×(-3);(2)(-7)×4;(3)(-3)×9;(4)(-3)×(-)
引导学生观察、分析例1中(4)小题两因数的关系,得出:有理数中仍然有:乘积是1的两个数互为倒数.
例2.见课本P30页
(六)分层练习,巩固提高。
(1)计算(口答):
①②③④
⑤⑥⑦⑧
四、课题小结
(1)有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。
(2)如何进行两个有理数的乘法运算:先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。
七年级数学《有理数的除法》教案 7
教学目标
1.使学生理解有理数除法的意义,掌握有理数除法法则,会进行有理数除法运算;
2.运用转化思想,理解有理数除法的意义,培养学生新旧知识之间联系的思维能力,通过乘除法之间的逆运算,培养学生逆向思维的能力,提高学生的计算能力,培养转化和全面分析问题的能力。
学情分析
本节课是学生在学习了有理数的基础上学习的,学生学起来比较容易
重点难点
1.教学重点:正确运用有理数除法法则进行有理数除法运算;
2.教学难点:理解零不能做除数,零没有倒数,寻找有理数除法转化为有理数乘法的方法和条件;
教学过程
有理数的除法
教学活动
活动1
有理数的除法
一、课前复习提问
1.有理数乘法法则;
2.有理数乘法的运算律:乘法交换律,乘法结合律,乘法分配律;
3.倒数的意义.
二、讲授新课
(一)有理数除法法则的推导
[问题]怎样计算8÷(-4)呢?
[提问]小学学过的除法的意义是什么?
得出 ①8÷(-4)=-2;又②8×( )=-2;于是有
③8÷(-4)=8×( )。
由此得出有理数除法法则:
除以一个不等于0的数,等于乘以这个数的倒数。
可以表示为:
a÷b=a· (b≠0) .
类似于乘法法则可得:
两数相除,同号得正,异号得负,并把绝对值相除,零除以任何一个不等于0的数,都得0。
对有理数除法法则的理解:
(1)法则所揭示的内容告诉我们,有理数除法与小学时学的除法一样,它是乘法的`逆运算,是借助“倒数”为媒介,将除法运算转化为乘法运算进行(强调,因为0没有倒数,所以除数不能为0);
(2)法则揭示有理数除法的运算步骤:第一步,确定商的符号,第二步,求出商的绝对值。
(二)有理数除法法则的运用
例1 计算:(1)(-36)÷9;
(2)( )÷( )。
强调:两数相除,先确定商的符号,再确定商的绝对值。
例2 化简下列分数:
(1) ; (2) .
强调:(1)符号法则;(2)一般来说,在能整除的情况下,往往采用法则的后一种形式,在确定符号后,直接除在不能整除的情况下,则往往将除数换成倒数,转化为乘法.
例3 计算:
(1)(-125 )÷(-5);
(2)-2.5÷ ;
(三)小结
1.通过小学除法意义的理解和类比,得出有理数除法法则,法则一:除以一个数等于乘以这个数的倒数,零不能做除数。法则二:两数相除,同号得正,异好号得负,并把绝对值相除;零除以任何一个不等于零的数都得零。
2.有理数的除法有两种方法,一般能整除时用第二种方法,强调要先确定结果的符号。
(四)教学反思
本节课是学生在学习了有理数乘法的基础上学习的,在小学的时候已经学习了两数的除法法则,所以这节课的内容对大部分学生来说,不是很难,他们只要会确定两数相除商的符号,然后在求商的绝对值就可以了。
七年级数学《有理数的除法》教案 8
教学目标
1.使学生理解有理数倒数的意义;
2.使学生掌握有理数的除法法则,能够熟练地进行除法运算;
3.培养学生观察、归纳、概括及运算能力。
教学重点和难点
重点:有理数除法法则。
难点:
(1)商的符号的确定。
(2)0不能作除数的理解。
教学手段
现代课堂教学手段
教学方法
启发式教学
教学过程
(一)、从学生原有认知结构提出问题
1.叙述有理数乘法法则。
2.叙述有理数乘法的运算律。
3.计算:
(1)3×(-2); (2)-3×5; (3)(-2)×(-5)。
(二)、导入新课
因为3×(-2)=-6,所以3x=-6时,可以解得x=-2;
同样-3×5=-15,解简易方程-3x=-15,得x=5。
在找x的值时,就是求一个数乘以3等于-6;或者是找一个数,使它乘以-3等于-15。已知一个因数的积,求另一个因数,就是在小学学过的除法,除法是乘法的逆运算。
三、讲授新课
1.有埋数的倒数
0没有倒数,(0不能作除数,分母是0没有意义等概念在小学里是反复强调的)
提问:怎样求一个数的倒数?
答:整数可以看成分母是1的分数,求分数的倒数是把这个数的分母与分子颠倒一下即可;求一个小数的倒数,可以先把这个小数化成分
数再求倒数。
什么性质
所以我们说:乘积为1的两个数互为倒数,这个定义对有理数仍然适用。
这里a≠0,同小学一样,在有理数范围内,0不能作除数,或者说0为分母时分数无意义。
2.有理数除法法则
利用有理数倒数的概念,我们进一步学习有理数除法。
因为(-2)×(-4)=8,所以8÷(-4)=-2。
由此,我们可以看出小学学过的除法法则仍适用于有理数除法,即
除以一个数等于乘以这个数的倒数。
0不能作除数。
例1 计算:
课堂练习
(1)写出下列各数的倒数:
(2)计算:
3.有理数除法的符号法则
观察上面的练习,引导学生总结出有理数除法的.商的符号法则:
两数相除,同号得正,异号得负。
掌握符号法则,有的题就不必再将除数化成倒数再去乘了,可以确定符号后直接相除,这就是第二个有理数除法法则:
两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不为0的数,都得0。
≠0).利用除法法则可以化简分数。
例2 化简下列分数:
例3 计算:
(4)(-7)÷3-20÷3(-7-20)÷3=(-27)÷3=-9。
(四)、小结
1.指导学生看书,重点是除法法则。
2.引导学生归纳有理数除法的一般步骤:
(1)确定商的符号;
(2)把除数化为它的倒数;
(3)利用乘法计算结果。
七年级数学《有理数的除法》教案 9
学习目标:
1、学会用计算器进行有理数的除法运算。
2、掌握有理数的混合运算顺序。
3、通过探究、练习,养成良好的学习习惯。
学习重点:
有理数的混合运算
学习难点:
运算顺序的确定与性质符号的处理
教学方法:
观察、类比、对比、归纳
教学过程
一、学前准备
1、计算
1)(—0.0318)÷(—1.4)2)2+(—8)÷2
二、探究新知
1、由上面的问题1,计算方便吗?想过别的方法吗?
2、由上面的问题2,你的计算方法是先算法,再算法。
3、结合问题1,阅读课本P36—P37页内容(带计算器的'同学跟着操作、练习)
4、结合问题2,你先猜想,有理数的混合运算顺序应该是?
5、阅读P36,并动手做做
三、新知应用
1、计算
1)、18—6÷(—2)×2)11+(—22)—3×(—11)
3)(—0.1)÷×(—100)
2、师生小结
四、回顾与反思
请你回顾本节课所学习的主要内容。
七年级数学《有理数的除法》教案 10
学习目标:
1、要熟记有理数除法的法则,会进行有理数除法的运算。
2、掌握求有理数倒数的方法,并能熟练地求出一个给定的有理数的倒数。
3、能熟练地进行简单的有理数的加减乘除混合运算。
4、体会比较、转化、分类的思想方法,在探索有理数除法法则时的应有
学习重点:
有理数除法的法则及应用;求一个有理数的倒数。
学习难点:
在进行有理数除法运算时,能根据题目特点,恰当地选择有理数的除法法则。
学习过程:
一、前置复习 :
1、有理数的乘法法则是:
举例说明。
2、多个有理数乘法:(1)几个不等于0的有理数相乘,积的符号由 决定,当 时积为正;当 时积为负。
(2)几个有理数相乘, ,积就为零。
二、探究新知:(教师寄语: 现实世界中的事物都是既相互联系又可以相互转化的,在数学上加与减,乘与除也是可以相互转化的)
自学课本58页至59页例4之前的内容,并且认真体会在探索除法与乘法的关系时,用到的比较、转化、分类的思想方法,一定要熟记:
(1) 有理数除法运算转化为乘法运算的法则:除以一个数,________________________。
____________________。
(2) 有理数的除法法则:两数相除,_____________,_____________,_____________。
0除以任何_______________________________。
(3) 与以前学过的倒数的概念一样,___________两个有理数互为倒数。
如,3与____互为倒数,-6与_____互为倒数,2.25是____的倒数,___是 的倒数。
三、新知应用:
例1、独立完成课本58页例4,然后对比课本上的.解答,思考交流:在两个________数相除时,可选择法则(1),在两个_______数相除时,可选择法则(2)
学以致用 计算:
(1) (42)7 (2) ( )( )
例2、计算(1) ( )( )( ) (2) ( )( )
(温馨提示:1、 有理数的乘除混合运算,应把除以一个数转化成乘这个数的倒数,然后统一成乘法来进行计算。2、 加减乘除混合运算的运算顺序和小学一样。)
四、课堂练习:独立完成课本P59练习2,3题。(将完整的计算过程写在下面空白处)
五、总结反思:
1、说一说:
本节课我学会了 ;
使我感触最深的是 ;
我感到最困难的是 ;
我想进一步探究的问题是 。
2、评一评
自我评价 小组评价 教师评价
【七年级数学《有理数的除法》教案】相关文章:
数学有理数的除法教案03-26
七年级数学有理数的除法的教案03-26
人教版数学有理数的除法教案设计03-26
关于有理数的除法教学教案10-08
七年级数学有理数教案09-30
小学数学除法教案06-08
小学数学除法的教案10-07
数学小数除法教案07-25
小学数学除法教案10-07